Universal Property of the Quotient Group

The universal property of the quotient group is a fact about the quotient group and group homomorphisms that is useful particularly in proving the first isomorphism theorem.

Theorem

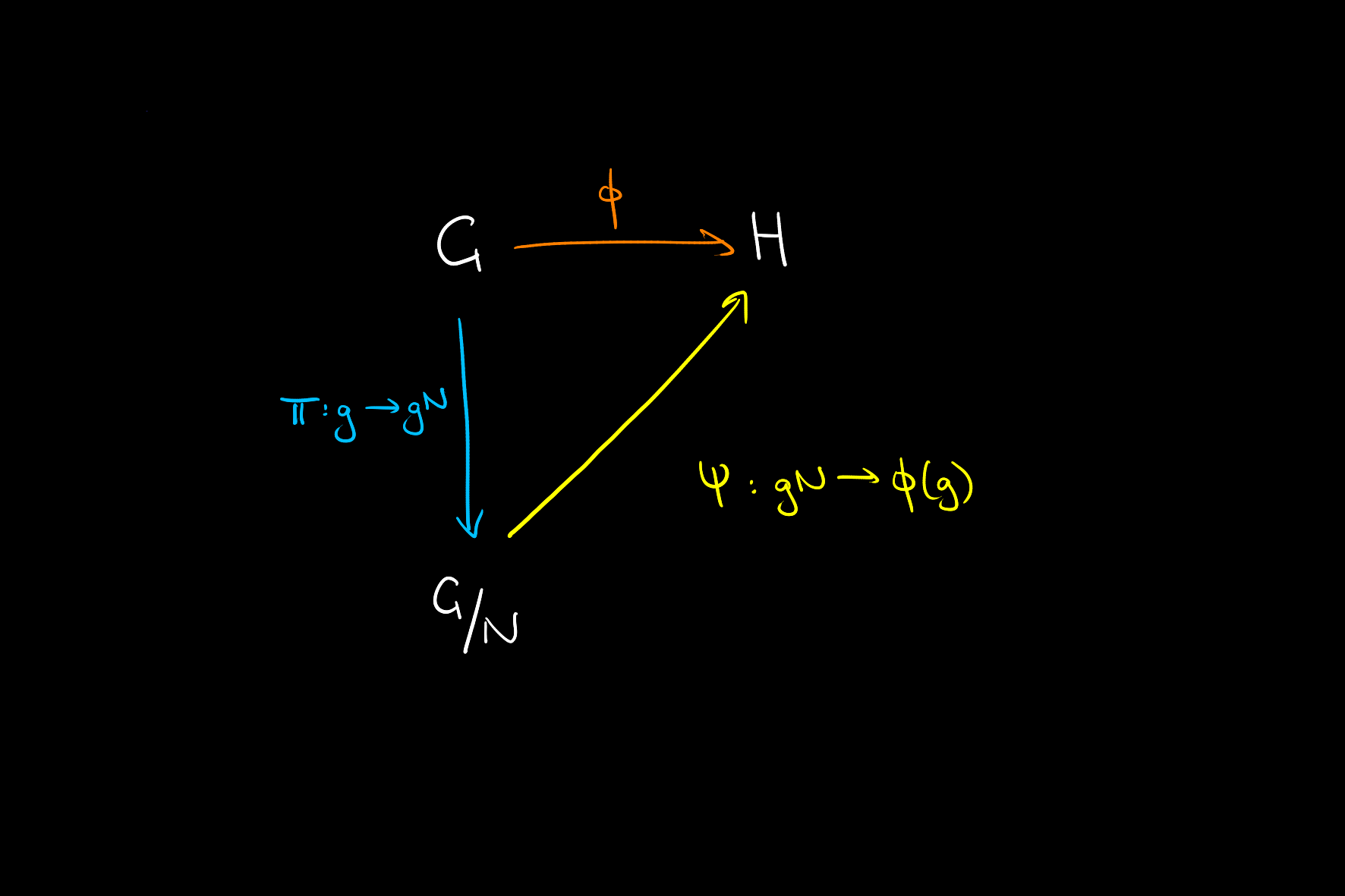
Let \(G\) and \(H\) be groups, and \(N\) be a normal subgroup of \(G\).

There is a bijection

\[ \Phi : \mathrm{Hom}(G/N, H) \to \left\{ \phi \in \mathrm{Hom}(G, H) : \phi(N) = \{0\} \right\}\]

given explicitly by

\[ \Phi : \psi \mapsto \psi \circ \pi\]

where \(\pi\) is the quotient epimorphism (natural projection onto the quotient group).

Furthermore, \(\ker(\phi) = \ker(\Phi(\phi))/N\).

While the map here is chosen in the direction where it is natural to define, in practice we wish to take a homomorphism \(G \to H\) and use this to define a homomorphism \(G/N \to H\).

Lemma

Let \(G\) and \(H\) be groups, and \(N\) be a normal subgroup of \(G\).

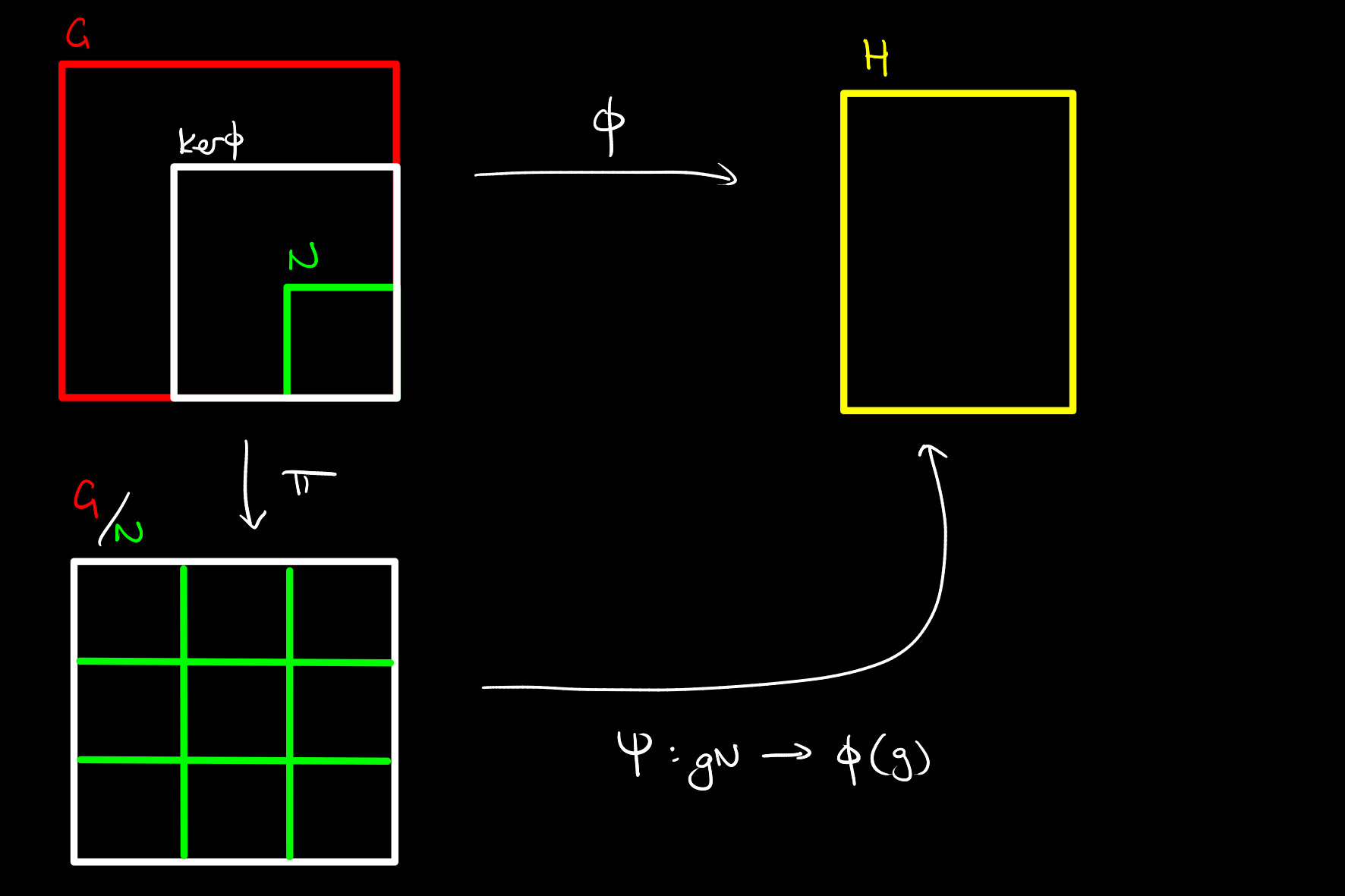
For any homomorphism \(\phi : G \to H\) satisfying \(\phi(N) = \{0\}\) there is a well defined homomorphism \(\psi : G/N \to H\) given by \(\psi(gN) = \phi(g)\) such that \(\psi \circ \pi = \phi\).

Intuitively, if a map vanishes on the normal subgroup \(N\), then there is no information lost when attempting to define an equivalent map from the quotient group \(G/N\), as elements of \(N\) are treated as identical.

We will first prove the lemma above.

Proof

We will prove this map \(\psi\) is well defined by showing if \(g\) and \(g'\) are in the same coset, then \(\phi(g) = \phi(g')\).

First note that by assumption \(\phi(n) = \mathrm{id}\) for any \(n \in N\). Let \(g \in g'N\), then \(g = g'n\) for some \(n \in N\) and hence

\[\begin{align*} \phi(g) &= \phi(g'n) \\ &= \phi(g')\phi(n) \\ &= \phi(g') \, \mathrm{id} \\ &= \phi(g'). \\ \end{align*}\]

Now, \(\psi\) is a homomorphism because \(\psi(gN)\psi(g'N) = gg' = \psi(gg'N)\).

Furthermore, \((\psi \circ \pi)(g) = \psi(gN) = \phi(g)\) for all \(g \in G\) and thus \(\psi \circ \pi = \phi\).

Now we prove the main result. In particular, note that the lemma above will give surjectivity of our map \(\Phi\).

Proof

Suppose that \(\psi \in \mathrm{Hom}(G/N, H)\). Then, we have that \(\Phi(\psi) = \psi \circ \pi\). Clearly as a composition of homomorphisms this is a homomorphism \(G \to N\), and if \(n \in N\) then \(\pi(n) = N\) and hence this composition vanishes on \(N\).

Surjectivity of \(\Phi\) follows from the lemma above.

Injectivity of \(\Phi\) comes about because if \(\Phi(\psi) = \Phi(\psi')\) then \(\psi \circ \pi = \psi' \circ \pi\), and for any element \(g \in G\), this means \(\psi(gN) = \psi'(gN)\). This implies that \(\psi = \psi'\).